Day 21 was a little bit of programming and a lot of discrete maths.

Part 1

I chose a "sparse" representation of points for this part, which turned out to be a lucky choice! The rocks in the garden is a Set of Positions, and the reachable places is another Set.

mkGrid :: String -> (Grid, (Position, Position))
mkGrid text = ( S.fromList [ V2 r c | r <- [0..maxR], c <- [0..maxC]
                           , rows !! r !! c == '#'
                           ]
              , (V2 0 0, V2 maxR maxC)
              )
  where rows = lines text
        maxR = length rows - 1
        maxC = (length $ head rows) - 1

findStart :: String -> Grid
findStart text = S.fromList [ V2 r c | r <- [0..maxR], c <- [0..maxC]
                            , rows !! r !! c == 'S'
                            ]
  where rows = lines text
        maxR = length rows - 1
        maxC = (length $ head rows) - 1

Simulation of a step is simple. For each reachable position after n steps, the positions after n+1 steps are its neighbours, unless there's a rock there. notAtRock handles the the case of positions that our outside the original map.

takeSteps :: Grid -> (Position, Position) -> Grid -> Grid
takeSteps rocks bounds places =
  S.filter (notAtRock rocks bounds) $ S.unions $ S.map adjacents places

notAtRock :: Grid -> (Position, Position) -> Position -> Bool
notAtRock rocks (_, V2 maxR maxC) (V2 r c) = here' `S.notMember` rocks
  where here' = V2 (r `mod` (maxR + 1)) (c `mod` (maxC + 1))

adjacents :: Position -> Grid
adjacents here = S.map (here ^+^) $ S.fromList [ V2 0 1, V2 1 0, V2 0 (-1), V2 (-1) 0 ]

With that, the simulation is done with iterate to lazily generate all futures of the simulation and picking out the step I want.

part1 rocks bounds start = S.size $ (!! 64) $ iterate (takeSteps rocks bounds) start

Part 2

Part 2 is a whole other beast. Simulating over 26 million steps, on an infinitely-repeating array of map tiles, is unfeasible. Luckily, there are several features of the well-designed input that lead to a much simpler solution.

The excellent explanation by Dazbo has good insights and prompted a lot of my solution. However, his uses the idea of finding the number of visited cells and fitting a quadratic curve to it. I wanted to use a more direct, geometric approach.

Some features of the problem make life simpler.

• Once a position has been reached, it continues to swap between reachable and not every step. The parity of a position is unchanged by different routes: the underlying square grid means that all paths to a point share the same parity.
• The size of the tiles (131 × 131), the starting point (the centre of the tile) and the empty horizontal and vertical channels mean that the elf can go from the centre of one tile to the centres of the four neighbouring tiles in exactly 131 steps. As all four directions are the the same, the area reached by the elf grows equally in all for directions.

The total number of steps taken is 202300 × 131 + 65. For my analysis, that's an even number of full-tile distances plus some change (half a tile). Therefore, the centre tile will be the same after all those steps as it is after 262 steps, and the nearby tiles that are an even number of tiles away will be the same. (Because the "change" part is no more than half a tile, I only need to extend one map tile beyond the completely-filled tiles.)

To make this a bit more concrete, I investigated what the patterns looked like with a 7×7 map tile, and taking n×7×2+3 steps. The solutions for 17 and 31 steps are shown below. You can see that many of the map tiles have the same patterns of occupation in both grids.

Things are a bit clearer if I abstract out the characters and use some colours, as shown below. Each square is a map tile. The diamond is the region reachable by the elf after n×7×2+3 steps for some n. The colours show the different regions of the extended map: the coloured regions in the two figures have identical map tiles. The central region is a chequerboard pattern of alternating "odd" and "even" tiles. The one- and three-tile "caps" at the top and bottom are the same. The two-vertical-tile coloured regions fill out the edges of the reachable area.

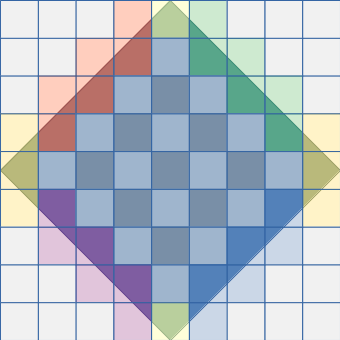
That gives me the path to the solution. I have to calculate the number of occupied spaces in each different region ("odd" filled, "even" filled, "top cap", "top-right edge", and so on). Then I need to calculate the number of each of those regions that will be present after a certain number of steps. I can then add them all up.

The first step is to simulate enough to have all the regions I want.

part2 rocks bounds start = ...
  where (V2 minR _, V2 maxR _) = bounds
        tileWidth = maxR - minR + 1
        (doubleTileSteps, extraSteps) = divMod 26501365 (tileWidth * 2)
        positions = (!! (tileWidth * 2 + extraSteps)) $ iterate (takeSteps rocks bounds) start
        ...

Then, finding the size of the regions.

I have a convenience function to count the number of occupied spaces in a map tile. Given the size of a map tile and a delta for where the particular map tile,  shiftBounds picks out the relevant tile and countInRange counts how many occupied spaces are there.

countInRange :: (Position, Position) -> Position -> Grid -> Int
countInRange bounds delta cells = 
  S.size $ S.filter (inRange (shiftBounds bounds delta)) cells

shiftBounds :: (Position, Position) -> Position -> (Position, Position)
shiftBounds (a, b) d = (a ^+^ d, b ^+^ d)

This is used a lot to add up all the different regions in the map.

evenFilled = countInRange bounds (V2 0 0) positions
oddFilled = countInRange bounds (V2 tileWidth 0) positions
upperPoint = countInRange bounds (V2 (tileWidth * -2) 0) positions
lowerPoint = countInRange bounds (V2 (tileWidth *  2) 0) positions
urEdge = countInRange bounds (V2 (- tileWidth) tileWidth) positions +
         countInRange bounds (V2 (- tileWidth * 2) tileWidth) positions

Finally, calculating the final area.

For a map tile size t and after 2t + e steps, I will have a pattern that looks like the smaller grid in the diagram above. For larger numbers of steps, expressed as 2nt + e (where n is a whole number), I will have

• (2n-1)² "even filled" tiles (the darker ones in the diagram above)
• (2n)² "odd filled" tiles (the lighter ones)
• 2n - 1 of each two-tile "edge" section
• 1 of each of the four "cap" pieces

part2 rocks bounds start = 
  nEvenFilled + nOddFilled + nEdges + upperPoint + lowerPoint + rCap + lCap
  where nEvenFilled = (doubleTileSteps * 2 - 1) ^ 2 * evenFilled
        nOddFilled = (doubleTileSteps * 2) ^ 2 * oddFilled
        nEdges = (doubleTileSteps * 2 - 1) * edges

And that's the solution!

Code

You can get the code from my locally-hosted Git repo, or from Gitlab.