Advent of Code 2024 day 5

Day 5 was one where the idea was simple enough, but turning it into a test that can be implemented took some care in thinking.

The logic

For part 1, I found it easier to express the test in terms of when a book was in an invalid order.

• A book is invalid if any page in the book is invalid.
• A page is invalid if any following page should have preceded this page.

That last condition I can express by knowing two things:

1. The set of pages which, if present, must precede this page
2. The set of pages that follow this page.

If those two sets have a non-empty intersection, this page is invalid.

That means I should work across the book in right-to-left order, keeping track of the pages that are known to follow a particular page. It also shows how I need to keep track of the ordering rules: if a page exists on the right-hand-side of some ordering rules, I need to find all the pages that exist on the left-hand-sides of those rules.

That determines the shape of the data structures I need to use.

Reading the input and making the rules

Reading the input is fairly simple. I parse the rules into just a list of pairs, leaving assembly of the rules for a later stage.

rulesBooksP = (,) <$> rulesP <* endOfLine <* endOfLine <*> booksP

rulesP = ruleP `sepBy` endOfLine
ruleP = (,) <$> decimal <* "|" <*> decimal

booksP = bookP `sepBy` endOfLine
bookP = decimal `sepBy` ","

The rules are a Map from page number (an Int) to a set of page numbers, giving the pages that must precede the given page. In other words, the keys of the map are the right-hand-sides of the rules, and the values are the left-hand-sides.

type Page = Int
type Rules = M.IntMap (S.Set Page)

mkRules :: [(Int, Int)] -> Rules
mkRules = foldr go M.empty 
  where go (a, b) m = M.insertWith S.union b (S.singleton a) m

Note that if a page number only exists on the left-hand-side of the rules, it will not appear in this Map (there are no constraints on what it must follow).

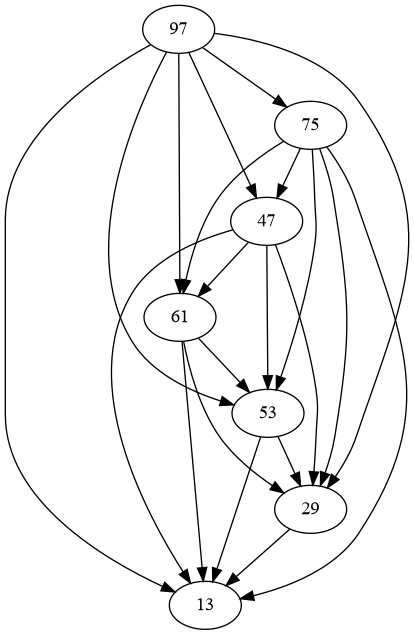
The rules define a precedence graph that looks like this (left for the example, right is my input).

Part 1

Following the logic above, I can express when a book is invalid. Walking along the pages from right to left is a foldr, where I keep track of two things:

1. Whether I've found the book to be invalid.
2. The pages that have followed this page.

Initially, the book is not invalid, and I've found no pages.

invalid :: Rules -> [Page] -> Bool
invalid rules book = fst $ foldr (pageInvalid rules) (False, S.empty) book

Finding if a page is invalid follows the test above.

The first clause of pageInvalid just propagates an earlier invalidation. The second clause does the work.

If this page has no conditions on what it must follow, it is by definition not invalid. Otherwise, it violates validity according to the condition above: if page following it is one that should precede it. (Yes, there are lots of double negatives in this reasoning.)

pageInvalid :: Rules -> Page -> (Bool, S.Set Page) -> (Bool, S.Set Page)
pageInvalid _rules _page (True, pages) = (True, pages)
pageInvalid rules page (False, pages) 
  | page `M.notMember` rules = (False, S.insert page pages)
  | otherwise = (violates, S.insert page pages)
  where preceders = rules ! page
        violates = not $ S.null $ S.intersection preceders pages

All that's left is the plumbing to extract the middle page numbers from the valid books.

part1 rules books = sum $ fmap middlePage validBooks
  where validBooks = filter (not . (invalid rules)) books

middlePage :: [Page] -> Page
middlePage b = b !! (length b `div` 2)

Part 2

I've now got to put invalid books into the correct order.

I do this by building up the book, left to right. At each point, I have to pick the page that comes next. A page is a printable now if:

1. There are no constraints on what must come before this page, or
2. No page that must come before this page is still to be printed.

That translates fairly directly into Haskell, if I know the rules about page ordering and the as-yet-unprinted pages in this book.

printable :: Rules -> S.Set Page -> Page -> Bool
printable rules unprinted page
  | page `M.notMember` rules = True
  | otherwise = S.null $ S.intersection preceders unprinted
  where preceders = rules ! page

That allows me to find the set of all printable pages at any point.

printCandidates :: Rules -> S.Set Page -> S.Set Page
printCandidates rules unprinted = 
  S.filter (printable rules unprinted) unprinted

And that allows me to reorder a book's pages. The unprinted pages are an unordered set; the printed pages are a list, to preserve order. I build up the book left to right. At each stage, I:

1. Find the candidate pages (those able to be printed)
2. Pick one, add it to the book sequence
3. Remove the page from the unprinted ones
4. Do the rest of the book.

I stop when I run out of unprinted pages.

reorder :: Rules -> [Page] -> S.Set Page -> [Page]
reorder rules printed unprinted 
  | S.null unprinted = printed
  | otherwise = reorder rules printed' rest
  where candidates = printCandidates rules unprinted
        next = S.findMin candidates
        rest = S.delete next unprinted
        printed' = printed ++ [next]

In doing this, I'm making some assumptions about the puzzle-setter ensuring the task is a good puzzle. Specifically, I assume that

1. Every set of pages has at least one valid ordering.
2. At some point in ordering the pages, it may be if that there is more than one page that could come next. If so, it doesn't matter which I choose.

It turns out, those assumptions are true!

Addendum: custom sorts

When I had a look at some of the solutions in the Reddit solutions megathread, I saw several people solving the problem by defining custom sorts on page numbers. I thought I'd have a go at that.

I can't define a newtype Page and then say it's an instance of Ord, as the ordering rules aren't known at compile time. But I can define a comparison function that takes the rules as well as two page numbers. pageOrder rules a b returns LT if a must be printed before b, GT if a must be printed after b, or EQ if there's no ordering constraint between them.

pageOrder :: Rules -> Page -> Page -> Ordering
pageOrder rules a b
  | S.member a rb = LT
  | S.member b ra = GT
  | otherwise = EQ
  where ra = M.findWithDefault S.empty a rules
        rb = M.findWithDefault S.empty b rules

However, we have to be careful! The ordering rules we're given may not define a complete ordering over all possible pages. The rules only define a local partial ordering relation between pairs of pages, but there's no guarantee that a ≤ b and b ≤ c implies a ≤ c. There may also be pairs of pages for which no ordering information is given; if so, what's the correct order?

For instance, given this input:

10|1
10|2

1,2,10

… we can say that the given book is in the wrong order, but both 10,1,2 and 10,2,1 are valid. Which should we choose?

However, if we stick with the assumption above, that possible alternative orderings don't affect the final answer (i.e. which is the middle page), we can make the books valid by sorting them.

part2 rules books = sum $ fmap middlePage reorderedBooks
  where invalidBooks = filter (not . valid rules) books
        reorderedBooks = fmap (sortBook rules) invalidBooks

sortBook :: Rules -> [Page] -> [Page]
sortBook rules pages = sortBy (pageOrder rules) pages

If we further assume that the rules given, taken locally, define a unique order of pages in each book, then a book is valid if the sorted pages are the same as the given pages.

valid :: Rules -> [Page] -> Bool
valid rules book = sortBook rules book == book

This is the case for my input.

If I don't make the unique order assumption, I need to revert to the earlier approach of testing each page in the book.

valid :: Rules -> [Page] -> Bool
valid rules book = fst $ foldr (pageValid rules) (True, []) book

pageValid :: Rules -> Page -> (Bool, [Page]) -> (Bool, [Page])
pageValid _rules _page (False, pages) = (False, pages)
pageValid rules page (True, pages) = (allowed, page:pages)
  where allowed = not $ any mustBeLaterThan pages
        mustBeLaterThan other = pageOrder rules page other == GT

Code

You can get the code from my locally-hosted Git repo, or from Codeberg. The original is as Main.hs, the version using the custom ordering is in MainOrdering.hs.