With Day 8, I did something shocking: I actually used the Linear library for some non-trivial vector arithmetic!
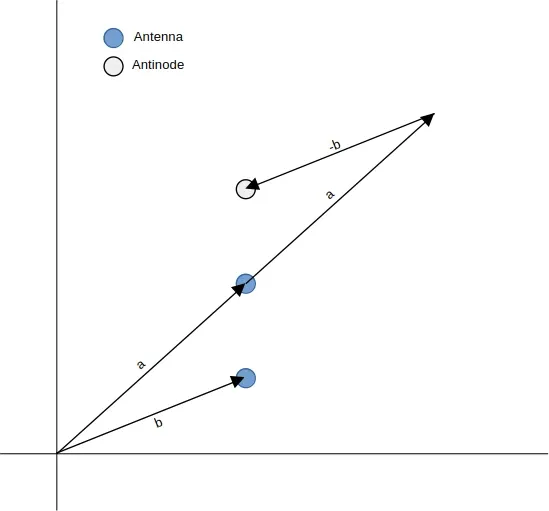
The idea is that, given two antennas a and b, both represented by vectors, b will induce an antinode on a at the position of a + a - b. If you swap a and b, you get the antinode on the other side.
Everything else builds around getting me to the place where I can make that calculation.
Data structure
I want a list of antenna positions, separated by frequency. That suggests a Map from frequency to list of positions.
type Position = V2 Int -- r, c
type Bounds = (Position, Position)
type Grid = M.Map Char [Position]Reading the grid is fairly straightforward: read the antennas into a list of (frequency, position) pairs, then fold over that to build the Map. I also return the bounds of the grid for later.
mkGrid :: String -> (Bounds, Grid)
mkGrid text = ((V2 0 0, V2 rMax cMax),
foldl' go M.empty points)
where rows = lines text
rMax = length rows - 1
cMax = (length $ head rows) - 1
points = [ (rows !! r !! c, V2 r c)
| r <- [0..rMax], c <- [0..cMax]
, rows !! r !! c /= '.'
]
go grid (f, pos) = M.insertWith (++) f [pos] gridFinding antinodes
I use a list comprehension to find all pairs of antennas (of the same frequency) and do the calculation on each pair, throwing away antinodes that are outside the grid. I apply that to all frequencies present.
allFreqAntinodes :: Bounds -> Grid -> Grid
allFreqAntinodes bounds = M.map (antinodesOf bounds)
antinodesOf :: Bounds -> [Position] -> [Position]
antinodesOf bounds ps =
filter (inRange bounds) [2 *^ a ^-^ b | a <- ps, b <- ps, a /= b]Combine and deduplicate the antinodes, and you've got the answer.
part1 bounds antennas = length $ nub $ concat $ M.elems $ allFreqAntinodes bounds antennasHarmonic antinodes
This is the same calculation as before, but I find the harmonic antinodes at $\mathbf{a} - k (\mathbf{a} - \mathbf{b}), k \in \mathbb{N}$. As antennas are at least one row or column apart, I can limit the number of harmonic antinodes I generate to the size of the grid. Many of those will be outside the grid, but the filter will take care of them.
harmonicAntinodesOf bounds@(_, V2 kMax _) ps =
filter (inRange bounds) [ a ^+^ k *^ (a ^-^ b)
| a <- ps, b <- ps, a /= b
, k <- [0 .. kMax]]That's all that's needed.
Code
You can get the code from my locally-hosted Git repo, or from Codeberg.