I did part 1 of day 13 with a little bit of brute force, before settling on a direct solution for part 2.

Data and parsing

The parsing here is a bit fiddly, so it's worth mentioning.

Each Machine is a record. Luckily, all the numbers fit in an Int.

type Position = V2 Int -- x, y

data Machine = Machine { buttonA :: Position
                       , buttonB :: Position
                       , prize :: Position 
                       }
  deriving (Show, Eq, Ord)

The sections of text and line breaks need some handling to get right. Thankfully, attoparsec makes this fairly simple to express.

buttonAP = V2 <$> ("Button A: X" *> signed decimal) <* ", Y" 
              <*> signed decimal <* endOfLine
buttonBP = V2 <$> ("Button B: X" *> signed decimal) <* ", Y" 
              <*> signed decimal <* endOfLine
prizeP   = V2 <$> ("Prize: X=" *> decimal) <* ", Y=" 
              <*> decimal

machineP = Machine <$> buttonAP <*> buttonBP <*> prizeP
machinesP = machineP `sepBy` (endOfLine <* endOfLine)

Note that the button parsers consume their trailing newline, but the prize parser doesn't. This allows the last record (that doesn't have a trailing newline) to be read.

Part 1

The problem's linear, so the order of interleaving the A and B presses doesn't matter: it's only the total number of them.

This was the brute force part. I tried pressing button A from 0 to 100 times, then found how many times to press button B to get the prize.

Given a machine and a certain number of presses of button A, findBPresses finds how many times to press B, returning Nothing if there's no solution. If finds how many times to press B to get the x value right, and the y value right, then checks if they're the same (and both are whole numbers).

findBPresses :: Machine -> Int -> Maybe (Int, Int)
findBPresses (Machine {..}) a 
  | nx == ny && mx == 0 && my == 0 = Just (a, nx)
  | otherwise = Nothing
  where aPos = a *^ buttonA
        V2 dx dy = prize - aPos
        V2 bx by = buttonB
        (nx, mx) = dx `divMod` bx
        (ny, my) = dy `divMod` by

findPresses finds all the solutions.

findPresses :: Machine -> [(Int, Int)]
findPresses m = catMaybes [ findBPresses m a | a <- [0..100] ]

Given a list of solutions, leastCost finds the least cost (or Nothing if there are none).

leastCost :: [(Int, Int)] -> Maybe Int
leastCost [] = Nothing
leastCost ps = Just $ minimum $ fmap (\(a, b) -> 3 * a + b) ps

A quick sum . catMaybes and you get the answer.

part1 = sum . catMaybes . fmap leastCost . fmap findPresses

Part 2

Part 2 was going to be too large for brute force, so I resorted to actually calculating the answer. I imagine two lines: one starting from the origin, doing presses of A; one starting from the prize, undoing presses of B. I need to find where these lines meet and work out how many presses of each button are needed.

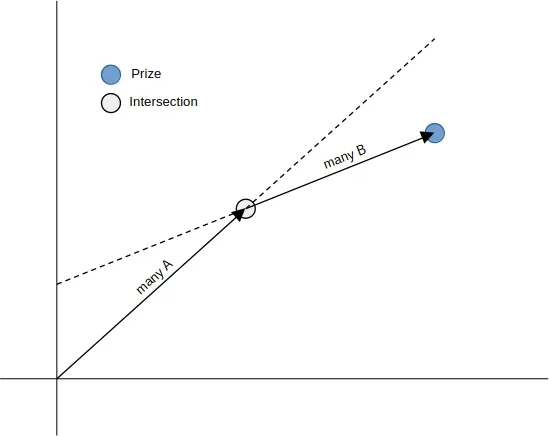
A quick check of the input file showed that no machine had collinear buttons, so there was always a unique solution. That saved some error checking.

isCollinear :: Machine -> Bool
isCollinear (Machine {..}) = slope buttonA == slope buttonB
  where 
    slope :: Position -> Rational
    slope (V2 x y) = (fromIntegral y) / (fromIntegral x)

The calculation of the intersection point comes straight from Wikipedia. Note that I'm using rational numbers here to represent the solution.

intersection :: Machine -> V2 Rational
intersection (Machine {..}) = V2 px py
  where V2 x2 y2 = buttonA
        V2 x4 y4 = prize
        V2 x3 y3 = prize ^-^ buttonB
        denom = fromIntegral (-x2 * (y3 - y4) - (-y2) * (x3 - x4))
        px = fromIntegral (-1 * (-x2) * (x3 * y4 - y3 * x4) ) / denom
        py = fromIntegral (-1 * (-y2) * (x3 * y4 - y3 * x4) ) / denom

From that, I can find the number of presses of each button. If both buttons are pressed a whole number of times, there's a valid solution.

findABPresses :: Machine -> Maybe (Int, Int)
findABPresses m@(Machine {..}) 
  | denominator na == 1 && denominator nb == 1 = 
      Just (fromInteger $ numerator na, fromInteger $ numerator nb)
  | otherwise = Nothing
  where 
    p = intersection m
    V2 dbx _dby = (enRat prize) ^-^ p
    V2 px _py = p 
    V2 ax _ay = enRat buttonA
    V2 bx _by = enRat buttonB
    na = px / ax
    nb = dbx / bx
    enRat :: Position -> V2 Rational
    enRat (V2 s t) = V2 (fromIntegral s) (fromIntegral t)

Code

You can get the code from my locally-hosted Git repo, or from Codeberg.