Advent of Code 2024 day 24 revisited

Now I've shaken off the virus I had over Christmas, it's time to have another look at the day 24 puzzle, this time attempting to solve it!

My earlier attempt used a lot of manual renaming of wires to guide a manual inspection of what the swaps should be.

Building on my earlier work, I could create a stage in the adder, showing what it should look like. I could also find the gates that should represent an adder stage, working back from a particular output.

The challenge was to identify where things went wrong.

A diagram of each stage of the adder should help.

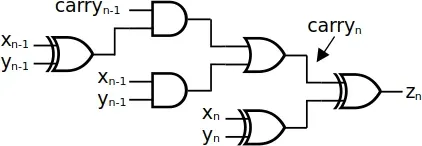
My idea was to build a stage of the adder, using the given gates, and to find when the gates provided didn't match the gate that should be in a particular position. This is possible because each gate in the adder stage is unique: starting at a particular carry input, there should be only one choice for each gate when building the adder I expect.

I anchor this process by relying on the first few adder stages. My earlier tests confirmed that the first seven (at least) stages of the adder were correct.

Fixing the adder is an inductive process. Given the carry from position n-1 (and all gates and wires preceding it) is correct, I can build up the adder until output n, by using the gates provided in the puzzle input. repairAdder does this, keeping a list of swapped wires as it goes. Note that the generated adder is an Either type: it's a Right DeviceTree if this adder stage is correct, or Left (String, String) if the two named wires need to be swapped. If this stage is correct, I can move on to the next stage; if not, I make the swap and try the current stage again.

repairAdder :: Device -> Int -> [(String, String)] -> [(String, String)]
repairAdder _device 44 acc = acc
repairAdder device n acc = 
  case adder of
        Left (o1, o2) -> repairAdder (swapWires o1 o2 device) n ((o1, o2) : acc)
        Right _ -> repairAdder device (n + 1) acc
  where d1 = replaceCarry (n - 1) device
        adder = growFromCarry n d1

The first step is to anchor that building process for a particular adder stage. I added another constructor to the GateType type, and wrote a function that replaced the carry sub-tree with a Carry gate (it finds the Or gate before the gate that produces the specified output).

data GateType = And | Or | Xor | Carry 
  deriving (Show, Eq, Ord)
  
replaceCarry :: Int -> Device -> Device
replaceCarry n device = (Gate Carry [] carryGate.output) : filter (/= carryGate) device
  where outWire = "z" ++ show2d n
        outGate = head $ filter ((== outWire) . output) device
        carryGate = head $ filter (\g -> (g.output `elem` outGate.inputs) && g.gType == Or) device

From that, I build up the adder in stages, as shown in the diagram below. growFromCarry does that building.

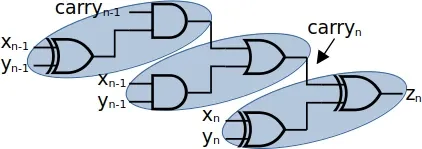
There's a bit of preamble to name all the inputs and outputs that should be seen in the adder stage. The spineGates show the structure of the adder stage to be built. Each highlighted pair in the diagram above is one stage in the building: the And gate on the spine and the Xor for the inputs is first, then the Or and And, finally the Xor and Xor. The work is done by growSpine, folding that list into the adder stage.

growFromCarry :: Int -> Device -> Either (String, String) DeviceTree
growFromCarry n device =
  do let c = Node {rootLabel = fromJust $ find ((== Carry) . gType) device, subForest = []}
     let x0 = "x" ++ show2d (n - 1)
     let y0 = "y" ++ show2d (n - 1)
     let x1 = "x" ++ show2d n
     let y1 = "y" ++ show2d n
     let z1 = "z" ++ show2d n
     let spineGates = [ (And, (Gate Xor [x0, y0] ""))
                      , (Or, (Gate And [x0, y0] ""))
                      , (Xor, (Gate Xor [x1, y1] ""))
                      ]
     grown <- foldM (growSpine device) c spineGates
     let grownOut = grown.rootLabel.output
     if grownOut == z1 then Right grown else Left (grownOut, z1)

This uses the fact that Either is a monad, behaving much like Maybe. So long as the monadic values are Right, computation proceeds; but the first Left (wrong) value stops and the whole computation returns that first Left value.

growSpine has the logic of finding the gates to build up the adder. It finds the gate that comes next in the spine, the new leaf gate, and the gate that comes next after the leaf. If these two "next" gates are the same, the wiring is correct. If growSpine can't find one or the other "next" gate, that indicates a wrong wire. In that case, it returns that the swap should occur between the output of the found node (the spine or the leaf) and the "other" wire in the found "next" node.

growSpine :: Device -> DeviceTree -> (GateType, Gate) -> Either (String, String) DeviceTree
growSpine device 
          spine 
          ( spineType  -- next spine template
          , (Gate leafType leafInput _) -- next leaf template
          )
  | null spineParents = Left (spineOut, otherParentInput)
  | null nextLeafParents = Left (nextLeaf.output, otherParentInput)
  | not $ null commonSpineCandidates = Right (Node {rootLabel = head commonSpineCandidates, subForest = [nextLeafTree, spine]})
  | otherwise = Left ("", "")
  where 
    spineParents = filter (\g -> g.gType == spineType && spineOut `elem` g.inputs) device
    nextLeaf = head $ filter (\g -> g.gType == leafType && leafInput == g.inputs) device
    nextLeafParents = filter (\g -> g.gType == spineType && nextLeaf.output `elem` g.inputs) device
    nextLeafTree = Node {rootLabel = nextLeaf, subForest = []}
    commonSpineCandidates = spineParents `intersect` nextLeafParents
    spineOut = spine.rootLabel.output
    otherParentInput = if null spineParents 
                        then head $ delete nextLeaf.output (inputs $ head nextLeafParents)
                        else head $ delete spineOut (inputs $ head spineParents) 

Example

Looking at the adder stage that feeds into z22 reveals this structure.

Gate {gType = Xor, inputs = ["gjn","kdh"], output = "z22"}
|
+- Gate {gType = And, inputs = ["x22","y22"], output = "kdh"}
|
`- Gate {gType = Or, inputs = ["hbc","wdr"], output = "gjn"}
   |
   +- Gate {gType = And, inputs = ["frt","mhw"], output = "wdr"}
   |  |
   |  +- Gate {gType = Xor, inputs = ["x21","y21"], output = "mhw"}
   |  |
   |  `- Gate {gType = Carry, inputs = [], output = "frt"}
   |
   `- Gate {gType = And, inputs = ["x21","y21"], output = "hbc"}

Comparison with the diagram above reveals that the and gate with output kdh is wrong: it should be an xor gate with the same inputs.

Building the adder stage from the Carry with the first two gates in the spine gives this structure.

Gate {gType = Or, inputs = ["hbc","wdr"], output = "gjn"}
|
+- Gate {gType = And, inputs = ["x21","y21"], output = "hbc"}
|
`- Gate {gType = And, inputs = ["frt","mhw"], output = "wdr"}
   |
   +- Gate {gType = Xor, inputs = ["x21","y21"], output = "mhw"}
   |
   `- Gate {gType = Carry, inputs = [], output = "frt"}

Now we have a problem adding the next gate in the spine. Wire gjn feeds into the correct xor gate, providing the output z22. But the other input to that gate, kdh, is an and gate when it should be the xor between x22 and y22. The xor gate in question has output wire hjf and fees into the adder stage for z23. That means that hjf and kdh should be swapped to make the z22 adder stage correct.

Building up the adder stages like this gives the correct swaps, at least for my input.

part2 :: Device -> String
part2 device = intercalate "," $ sort $ concatMap (\(a, b) -> [a, b]) swaps
  where swaps = repairAdder device 3 []

Finally! The puzzle is solved by a program.

Code

You can get the code from my locally-hosted Git repo, or from Codeberg. MainOriginal.hs is the original solution where I manually solved the problem. MainWithInvestigations.hs is a version of the code above that includes additional code I wrote to investigate the adder and develop the solution. Main.hs is the final version that has only what's needed for this solution.