Advent of Code 2023 day 20

Day 20 was the first occurrence of a key feature of the Haskell way of doing things, the reader-writer-state monad stack, the RWS. In this case, the reader is the topology of the network, the writer is a log of the broadcast messages, and the state is the combination of the states of the modules and the current queue of messages.

Data structures and parsing

As usual, I define new structures for holding the data. A Pulse has a source, a Level, and a destination; pulses are held in a Queue, where new pulses are fed in from the right and extracted from the left (this is the same order as they're presented in the input rules).

type Name = String

data Level = Low | High deriving (Show, Eq, Ord)
data Pulse = Pulse { _source :: Name, _level :: Level , _destination :: Name }
  deriving (Show, Eq, Ord)
makeLenses ''Pulse  

type Queue = Q.Seq Pulse

A Module is one of the four types. FlipFlops hold a boolean state, Conjuctions have a Memory that connects source to last-seen state.

type Memory = M.Map Name Level

data Module = 
  Broadcast 
  | FlipFlop Bool 
  | Conjunction Memory
  | Untyped
  deriving (Show, Eq, Ord)

The Network is the connections from modules to modules. The Modules are held in a Map, indexed by name. The NetworkState holds both the current modules and the message queue. Finally, a NetworkHandler combines the Network reader, the list of Pulses writer, and the NetworkState.

type Network = M.Map Name [Name]
type Modules = M.Map Name Module

data NetworkState = NetworkState { _modules :: Modules
                                 , _queue :: Queue
                                 }
  deriving (Show, Eq, Ord)
makeLenses ''NetworkState  

type NetworkHandler = RWS Network [Pulse] NetworkState

Parsing the data follows the rules as they're given in the input file.

configLinesP :: Parser [((Module, Name), [Name])]
configLineP :: Parser ((Module, Name), [Name])
moduleP, broadcastP, flipFlopP, conjunctionP :: Parser (Module, Name)
nameP :: Parser Name

configLinesP = configLineP `sepBy` endOfLine
configLineP = (,) <$> (moduleP <* " -> ") <*> (nameP `sepBy` ", ")

moduleP = broadcastP <|> flipFlopP <|> conjunctionP

broadcastP = (Broadcast, "broadcaster") <$ "broadcaster"
flipFlopP = (FlipFlop False, ) <$> ("%" *> nameP)
conjunctionP = (Conjunction M.empty, ) <$> ("&" *> nameP)

Each line of the input turns into a pair, comprising the pair of module type and module name, and the list of names of modules it feeds into. Unfortunately, this isn't at all like the structures I need for the simulation of the network.

I build the Network and Modules in several passes (hardly efficient, but easy to write and quick enough). They are

1. creating the network (and initial stab at the modules)
2. creating the modules
3. adding the memory to all the Conjunction modules

assembleNetwork :: [((Module, Name), [Name])] -> (Network, Modules)
assembleNetwork config = (network, modules)
  where (network, modules0) = mkNetwork config
        modules1 = M.union (mkModules config) modules0
        modules = addConjunctionMemory network modules1

Making the network walks over the config lines, creating a connection from each source module name to the list of destinations. It also creates an Untyped module for each destination. Making the modules builds a Map from the module type and name given in each config line. These two collections of Modules are combined in assembleNetwork above, so that unspecified destinations are present as Untyped modules.

mkNetwork :: [((Module, Name), [Name])] -> (Network, Modules)
mkNetwork config = (net, mods) 
  where net = M.fromList $ fmap (\((_, n), ds) -> (n, ds)) config
        mods = M.fromList $ concatMap (\(_, ds) -> fmap (\d -> (d, Untyped)) ds) config

mkModules :: [((Module, Name), [Name])] -> Modules
mkModules = M.fromList . fmap (\((m, n), _) -> (n, m))

Finally, I add the full memories to all the Conjuctions. This is a pair of nested folds: for each entry in the Network, and for each destination in the entry, if the destination is a Conjunction, add that source to the destination's memory.

addConjunctionMemory :: Network -> Modules -> Modules
addConjunctionMemory network modules = 
  M.foldlWithKey addMemory modules network

addMemory :: Modules -> Name -> [Name] -> Modules
addMemory modules source connections = 
  foldl' (addOneMemory source) modules connections

addOneMemory :: Name -> Modules -> Name -> Modules
addOneMemory source modules destination =
  case modules ! destination of
    Conjunction memory -> 
      M.insert destination 
               (Conjunction $ M.insert source Low memory) 
               modules
    _ -> modules

Simulating the network

Now I have everything assembled, I can do some simulation!

The rules of the simulation are implemented in processPulse. This takes a Pulse and a Module and returns the updated Module and the optional Level of any new Pulse. Almost all the logic is handled by pattern matching.

processPulse :: Pulse -> Module -> (Module, Maybe Level)
processPulse (Pulse _ l _) Broadcast = (Broadcast, Just l)
processPulse (Pulse _ Low _) (FlipFlop False) = (FlipFlop True, Just High)
processPulse (Pulse _ Low _) (FlipFlop True) = (FlipFlop False, Just Low)
processPulse (Pulse _ High _) (FlipFlop s) = (FlipFlop s, Nothing)
processPulse (Pulse s l _) (Conjunction memory) = 
  (Conjunction memory', Just outLevel)
  where memory' = M.insert s l memory
        outLevel = if all (== High) $ M.elems memory' then Low else High
processPulse _ Untyped = (Untyped, Nothing)

handlePulse takes one Pulse and uses the result of processPulse to update the state according to the network structure. It uses lenses to get into the innards of the nested structures, but is mostly just moving data around from place to place.

handlePulse :: Pulse -> NetworkHandler ()
handlePulse p@(Pulse _ _ destination) = 
  do  mdl <- gets ((! destination) . _modules)
      outGoings <- asks (! destination)
      let (mdl', maybeLevel) = processPulse p mdl
      modify (\s -> s & modules . ix destination .~ mdl')
      tell [p]
      case maybeLevel of
        Nothing -> return ()
        Just level' -> 
          do let newPulses = fmap (Pulse destination level') outGoings
             modify (\s -> s & queue %~ (>< (Q.fromList newPulses)))

handlePulses keeps calling handlePulse until the queue is empty. buttonPress sets the queue to a button press, then simulates.

handlePulses :: NetworkHandler ()
handlePulses = 
  do  pulses <- gets _queue
      case pulses of
        Q.Empty -> return ()
        (p :<| ps) -> 
          do modify (\s -> s & queue .~ ps)
             handlePulse p
             handlePulses

buttonPress :: Network -> NetworkState -> (NetworkState, [Pulse])
buttonPress network state = 
  execRWS handlePulses network (state & queue .~ pulse0)
  where pulse0 = Q.singleton $ Pulse "button" Low "broadcaster"    

Solving the puzzle

Now I can finally solve the puzzles!

Both parts of the puzzle require me to look at the log of button presses and extract some information, so I have a function that does that. pressAndEvaluate takes an interim result, presses the button, and combines the log with the interim result to generate a new result. For part 1, the combination is to count the number of high and low pulses.

part1, part2 :: Network -> Modules -> Int
part1 network modules = highs * lows 
  where (_, (highs, lows)) = 
         (!! 1000) $ iterate (pressAndEvaluate network part1Extractor) (state0, (0, 0))
        state0 = NetworkState modules Q.empty

pressAndEvaluate :: Network -> (a -> [Pulse] -> a) -> (NetworkState, a) -> (NetworkState, a)
pressAndEvaluate network resultExtractor (state0, result0) = (state1, result1)
  where (state1, pulses) = buttonPress network state0
        result1 = resultExtractor result0 pulses

part1Extractor :: (Int, Int) -> [Pulse] -> (Int, Int)
part1Extractor (highs, lows) pulses = (highs + length hs, lows + length ls)
  where (hs, ls) = partition ((== High) . _level) pulses

Part 2 needs a Low pulse sent to the the rx node. Inspection of the network graph shows that rx is supplied only by the Conjuction module lx, and this has four inputs. That means lx will only send a Low pulse when each of these inputs sends it a High pulse. Each of those inputs comes from a separate chunk of the network, and these chunks are only connected by the broadcaster and lx modules.

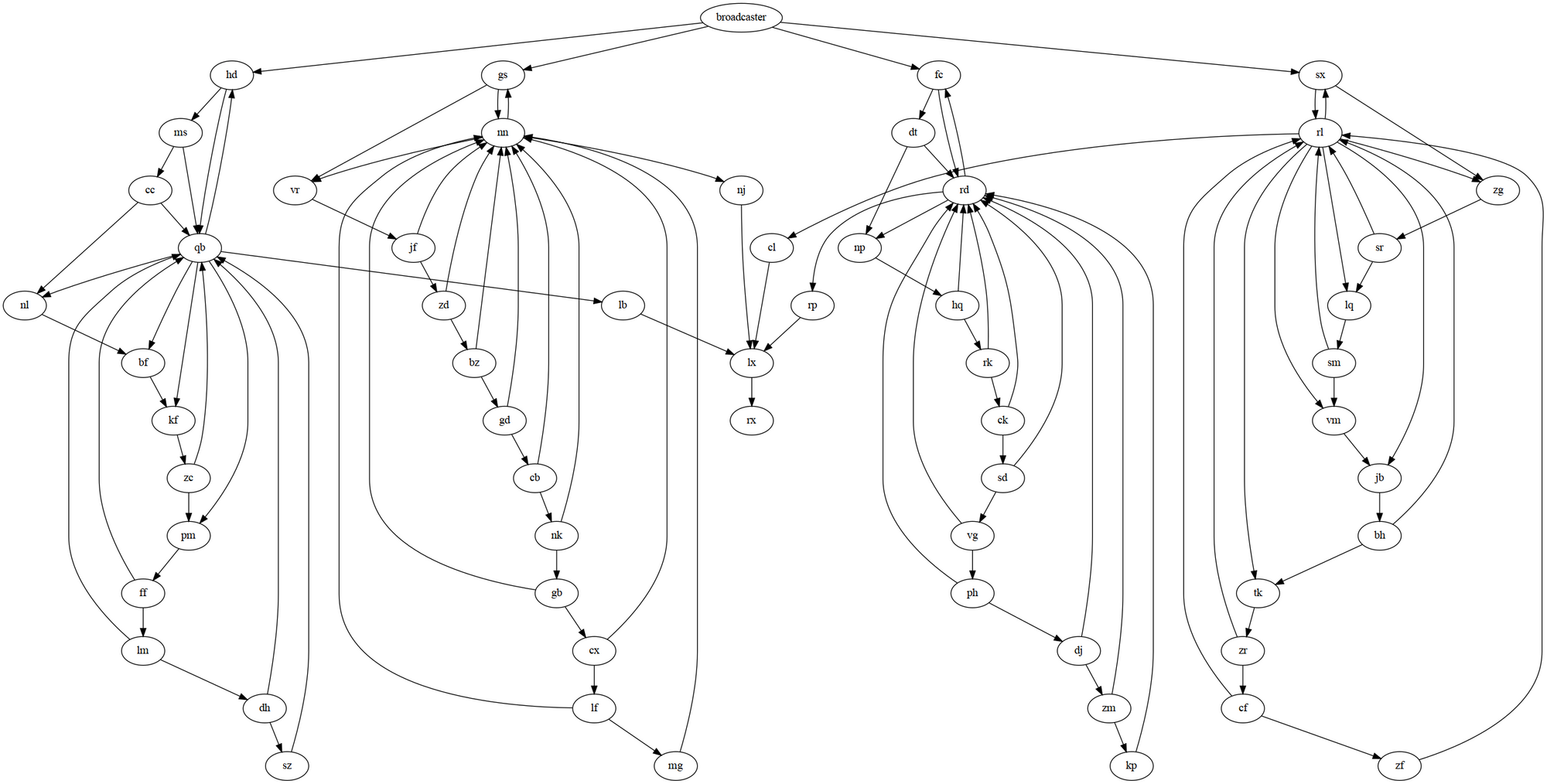
Running the network for 10,000 steps shows that each of these chunks sends a High pulse every few thousand-ish button presses, and there's no burn-in time for any of them. This is the same as the loops for day 8, and I take the same approach here.

For part 2, the extractor pulls out High pulses going to lx. Once I have those, I do some list-processing shennanigans to find the button press of the first high pulse sent by each, and find the lowest common multiple of the four values.

part2 network modules = foldl' lcm 1 cycleLengths
  where (_, lxPulses) = 
         (!! 10000) $ iterate (pressAndEvaluate network part2Extractor) (state0, [(0, [])])
        state0 = NetworkState modules Q.empty
        lxHighs = filter (not . null . snd) lxPulses
        cycleLengths = fmap ((fst . head) . sort) $ 
                          groupBy ((==) `on` (_source . snd)) $ 
                          sortBy (compare `on` (\(_, p) -> p ^. source)) $ 
                          fmap (\(n, ps) -> (n, head ps)) lxHighs 

part2Extractor :: [(Int, [Pulse])] -> [Pulse] -> [(Int, [Pulse])]
part2Extractor allRs@((i, _):rs) pulses = (i + 1, lxPulses) : allRs
  where lxPulses = filter catchLx pulses
        catchLx (Pulse _ High "lx") = True
        catchLx _ = False

Code

You can get the code from my locally-hosted Git repo, or from Gitlab.